
Higher tier only
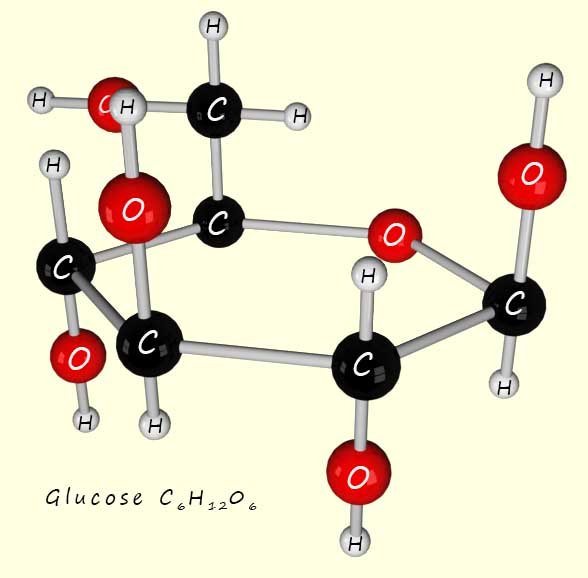
Glucose (shown opposite) has the molecular formula C6H12O6, the numbers in its molecular formula tell you the molar ratio of each element present in the compound. So for example water has the molecular formula H2O, this indicates that there are 2 moles of hydrogen for every one mole of oxygen present in water molecules. Or for glucose there are 6 moles of carbon, 12 moles of hydrogen and 6 moles of oxygen atoms present in one mole of glucose molecules.
You can also work backwards, so for example if you are given the masses of elements present in a compound you can easily calculate the formula for this compound.
Example 1. When a compound containing the metal zinc and non-metal oxygen was broken down into its elements, 6.5g of zinc
and 1.6g of oxygen were obtained. Calculate the formula for this ionic compound. To calculate the formula for zinc oxide follow the steps below:
Step 1 - Using the masses given in the question calculate the number of moles of each element produced -
use the appropriate formula from the box shown below:
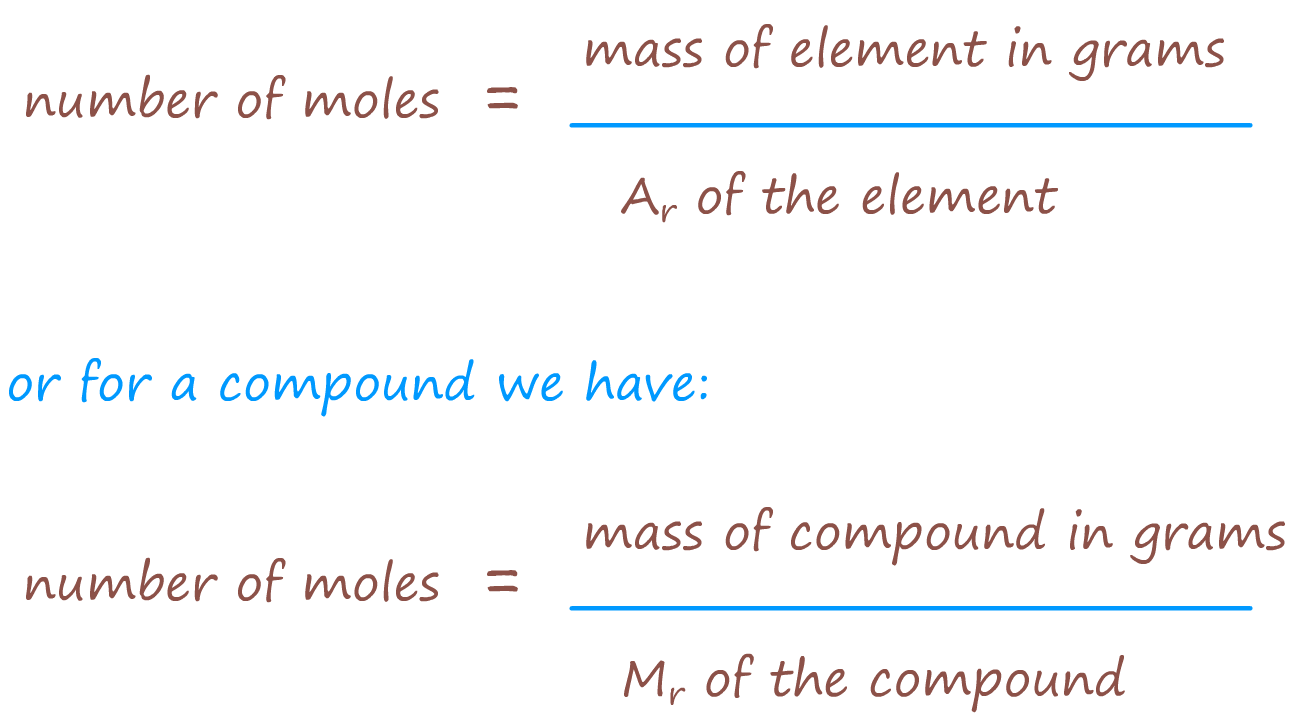
So for our example using the masses given in the example above we have:
| moles of zinc: 6.5g/65 = 0.1 moles | moles of oxygen: 1.6g/16 = 0.1 moles |
Step 2- The final step is simply to cancel the number of moles down to the simplest ratio possible. To do this divide by the smallest number of moles present. Since number of moles is the same for both zinc and oxygen, simply divide both by 0.1
| moles of zinc: 0.1 moles/0.1 = 1 | moles of oxygen: 0.1 moles/0.1 = 1 |
So the ratio of the number of moles of zinc to oxygen is 1:1, so the formula is simply ZnO - simple!

Being asked to find the empirical formula for a compound is a common exam question, the empirical formula is the simplest whole number ratio of each element present in a compound and it is very easy to calculate.
The empirical formula is usually found from experimental data. As an example consider the sugar glucose, its molecular formula as shown above is C6H12O6, however we can simplify this formula down by dividing by 6 to give: C1H2O1 or simply CH2O. This "simplest" formula is called the empirical formula. This empirical formula could represent any number of substances e.g. by multiplying it by 2 we get C2H4O or by multiplying by 3 we get C3H6O3. To get the actual molecular formula from the empirical formula you need the relative molecular mass (Mr) of the compound. Glucose has a Mr of 180; now the Mr of the empirical formula CH2O is 30. So if we divide 180 by this mass (180/30 = 6) then this tells you that in order to get the actual molecular formula you need to multiply the empirical formula by 6.
A sample of magnesium ribbon, mass 1.2g was placed inside a crucible and heated strongly using a Bunsen burner until all the magnesium had completely oxidised and formed magnesium oxide. The crucible was allowed to cool and the mass of the magnesium oxide formed was found to be 2g. How can we calculate the empirical formula of the magnesium oxide formed? Simply follow the steps listed in the table below:
| write out the symbols for each element preset | Mg | O |
|---|---|---|
| mass of each element present | 1.2g | 0.8g |
| divide masses by Ar to get number of moles present | 1.2g/24= 0.05 | 0.8g/16 = 0.05 |
| divide by the smallest number of moles to get ratio (since in this case both numbers are the same we divide by 0.05) | 0.05/0.05 = 1 | 0.05/0.05 = 1 |
| empirical formula | empirical formula is MgO | |
Example 3 - A hydrocarbon molecule has a Mr of 84. It is known that 72g of its mass is due to carbon.
Find the empirical and molecular formula for this hydrocarbon molecule.
If the molecule has a molar mass of 84g and 72g are due to carbon, then 12g must be due to the hydrogen present in the molecule. So simply
use the method above to calculate the molecular formula of the hydrocarbon:
| write out the symbols for each element preset | C | H |
|---|---|---|
| mass of each element present | 72g | 12g |
| divide masses by Ar to get number of moles present | 72/12 = 6 | 12/1 = 12 |
| divide by the smallest number of moles to get ratio, the smallest number of moles present is 6. | 6/6 = 1 | 12/6 = 2 |
| empirical formula | empirical formula is CH2 | |
The empirical formula CH2 has a Mr of 14. The Mr of the compound is known to be 84. So 84/14 = 6. So to get the molecular formula the empirical formula needs to be multiplied by 6. This gives a molecular formula of C6H12.
You may also come across questions where instead of being given masses for the reactants and products to work out an empirical formula you may instead be given percentages e.g.
Example 3b - A compound has a composition of 49.3% carbon, 6.9% hydrogen, and 43.8% oxygen by mass. Calculate its empirical formula and determine its molecular formula if the molar mass is 146g.
Simply follow the method in the table below, which is very similar to the method shown above to work out the empirical formula.
| write out the symbols for each element preset | C | H | O |
|---|---|---|---|
| % of each element present | 49.3% | 6.9% | 43.8% |
| assume you have 100g of the substance so % will become grams- or mass of each element present | 49.3g | 6.9g | 43.8g |
| divide masses by Ar to get number of moles present | 49.3/12 = 4.1 | 6.9/1 = 6.9 | 43.8/16 = 2.74 |
| divide by the smallest number of moles to get ratio, the smallest number of moles present is 2.74. | 4.1/2.74 = 1.5 | 6.9/2.74 = 2.5 | 2.74/2.74 = 1 |
| empirical formula | empirical formula is C1.5H2.5O
To remove decimals double all the numbers to give: C3H5O2 |
||
The empirical formula is C3H5O2 which gives a Mr = 73, however in the original question the molecular mass of the compound was given as 146; now this is simply double the mass of the empirical formula so the actual molecular formula for the unknown compound is simply C6H10O4.
Test your understanding of empirical formula by completing the questions in the quiz below:
Work out the empirical formula for the compounds in the quiz below; check your answers as you go.
Example 4 - 32g of methane (CH4) was combusted in 128g of oxygen to produce 88g of carbon dioxide and 72g of water vapour. Write a balanced symbolic equation for this reaction using the reacting masses given in the question.
Now you may be able to simply write the balanced symbolic equation if you have seen this combustion reaction before, but that is NOT the point of this example. You need to use the reacting masses in the example given to calculate the mole ratios, that is the purple a,b,c and d numbers in the equation above, for each of the reactants and products, to do this use the method shown below:
Ar of C=12 Ar of H=1 Ar of O=16
| substance | methane (CH4) | oxygen (O2) | carbon dioxide (CO2) | hydrogen oxide (H2O) |
|---|---|---|---|---|
| Mr | 12 + 4 = 16 | 16 × 2 = 32 | 12 + 32 = 44 | 2 + 16 = 18 |
Step 2- Divide the mass of each substance present by its Mr to calculate the number of moles present:
| substance | methane (CH4) | oxygen (O2) | carbon dioxide (CO2) | hydrogen oxide (H2O) |
|---|---|---|---|---|
| mass/Mr | 32/16 | 128/32 | 88/44 | 72/18 |
| number of moles | 2 | 4 | 2 | 4 |
Step 3- Divide by the smallest number of moles present. In this case the smallest number of moles present is 2 moles, so divide by 2 to get a mole ratio, this will provide the "numbers" to go in front of the reactants and products in the balanced symbolic equation.
| substance | methane (CH4) | oxygen (O2) | carbon dioxide (CO2) | hydrogen oxide (H2O) |
|---|---|---|---|---|
| mass/Mr | 32/16 | 128/32 | 88/44 | 72/18 |
| number of moles | 2 | 4 | 2 | 4 |
| divide by 2 to get mole ratio | 1 | 2 | 1 | 2 |
The bottom row in the table gives the mole ratio for each of the reactants and products in the balanced symbolic equation,
so simply put these into the equation:
Example 5 - 8g of iron(III) oxide (Fe2O3) was reduced by 4.2g of carbon monoxide to produce 5.6g of iron
and 6.6g of carbon dioxide. Work out a balanced equation for this reaction.
Ar of C=12 Ar of H=1 Ar of O=16 Ar of Fe=56
Method is identical to the one above:
Step 1 - Work out the Mr for each of the reactants and products in the reaction.
| substance | iron (III) oxide (Fe2O3) | carbon monoxide (CO) | iron (Fe) | carbon dioxide (CO2) |
|---|---|---|---|---|
| Mr | (56 × 2) + (16 × 3) = 160 | 16 + 12 = 28 | 56 | 12 + 32 = 44 |
Step 2- divide the mass of each of the reactants and products by its Mr/Ar to calculate the number of moles present.
| substance | iron (III) oxide (Fe2O3) | carbon monoxide (CO) | iron (Fe) | carbon dioxide (CO2) |
|---|---|---|---|---|
| mass/Mr | 8/160 | 4.2/28 | 5.6/56 | 6.6/44 |
| number of moles present | 0.05 | 0.15 | 0.1 | 0.15 |
Step 3- divide by the smallest number of moles present to get the mole ratio:
| substance | iron (III) oxide (Fe2O3) | carbon monoxide (CO) | iron (Fe) | carbon dioxide (CO2) |
|---|---|---|---|---|
| number of moles present | 0.05 | 0.15 | 0.1 | 0.15 |
| mole ratio | 0.05/0.05 = 1 | 0.15/0.05 = 3 | 0.1/0.05 = 2 | 0.15/0.05 = 3 |
So we have:
